삼각비
직각삼각형의 변들 사이의 비율은 삼각비라고 합니다. 널리 알려진 세 가지 삼각비는 사인 (sin), 코사인 (cos), 그리고 탄젠트 (tan) 입니다. 이들은 예각 에 대하여 아래에 정의직각삼각형의 변들 사이의 비율은 삼각비라고 합니다.


특수각 삼각비 : 흔히 사용하는 특수각 0º 30º 45º 60º 90º에 대한 삼각비를 쉽게 구할 수 있습니다.
삼각비에는 자주 사용하는 특수각의 삼각비 값이 존재합니다.

표를 보시면 특별한 성질이 있음을 알 수 있는데
sin은 각이 커질수록 그 값이 커지고 cos은 각이 커질수록 값이 작아지며 tan은 각이 커질수록 값이 커지고 있지만 90º가 되는 순간 그 값을 구할 수 없게 됩니다.
삼각함수
삼각비는 직각삼각형에서 직각 이외의 다른 한 각이 주어지면 세 변의 길이의 비를 알 수 있다는 것에서 착안되어 만들어 진 것이라면, 삼각함수는 삼각비의 개념을 앞서 배운 일반각으로 확장한 것입니다.
앞서 일반각에서 나온 동경 OP 좌표평면의 원점을 중심으로 회전하면서 원을 그리게 됩니다. 따라서 삼각함수는 원과 관련이 있고 원 위의 점 P의 좌표가 삼각함수의 값을 결정하게 됩니다.

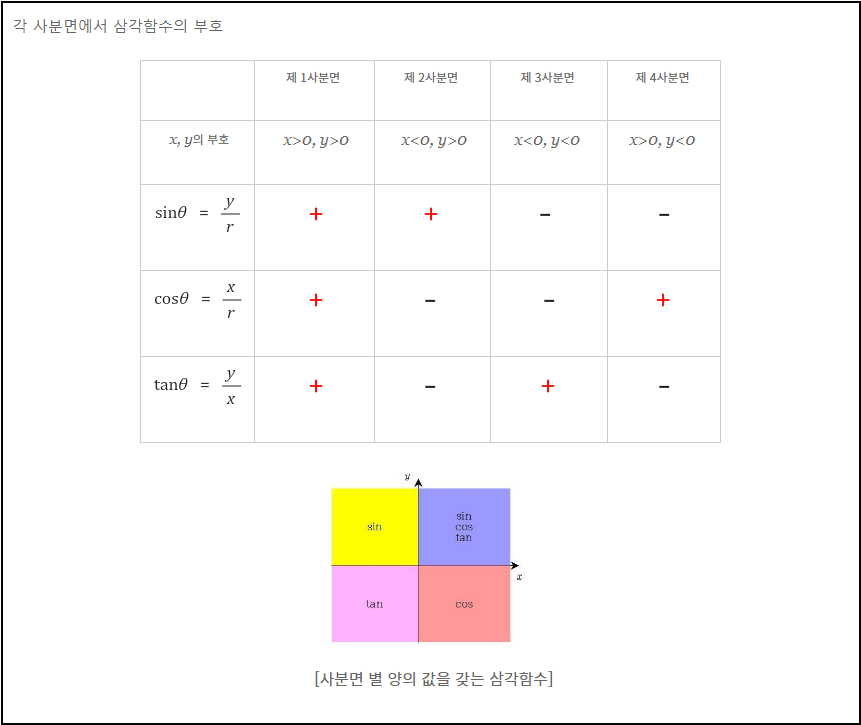
앞에서 다룬 삼각함수의 정의를 이용하여 좌표평면 위의 각 사분면에서 삼각함수의 부호를 알아보도록 하겠습니다.
정의로 부터 삼각함수는 각각

로 표현되는 것을 알았습니다.
삼각함수는 동경 OP의 점 P(x, y)의 좌표에 의해 정해지므로 각 사분면에서 부호를 생각해보면
제 1사분면 : x>0, y>0 제 2사분면 : x<0, y>0
제 3사분면 : x<0, y<0 제 4사분면 : x>0, y<0
이므로 제 1사분면에서는 세 가지모두 양수이고, 제 2사분면에서는 sin, 제 3사분면에서는 tan,제 4사분면에서는 cos이 양수가 됩니다.